More than a quarter billion people today are infected with the hepatitis B virus (HBV), the World Health Organization estimates, and more than 850,000 of them die every year as a result. Although an effective and inexpensive vaccine can prevent infections, the virus, a major culprit in liver disease, is still easily passed from infected mothers to their newborns at birth, and the medical community remains strongly interested in finding better ways to combat HBV and its chronic effects. It was therefore notable last month when Reidun Twarock, a mathematician at the University of York in England, together with Peter Stockley, a professor of biological chemistry at the University of Leeds, and their respective colleagues, published their insights into how HBV assembles itself. That knowledge, they hoped, might eventually be turned against the virus.

Their accomplishment has gained further attention because only this past February the teams also announced a similar discovery about the self-assembly of a virus related to the common cold. In fact, in recent years, Twarock, Stockley and other mathematicians have helped reveal the assembly secrets of a variety of viruses, even though that problem had seemed forbiddingly difficult not long before.

Their success represents a triumph in applying mathematical principles to the understanding of biological entities. It may also eventually help to revolutionize the prevention and treatment of viral diseases in general by opening up a new, potentially safer way to develop vaccines and antivirals.

A Geodesic Insight

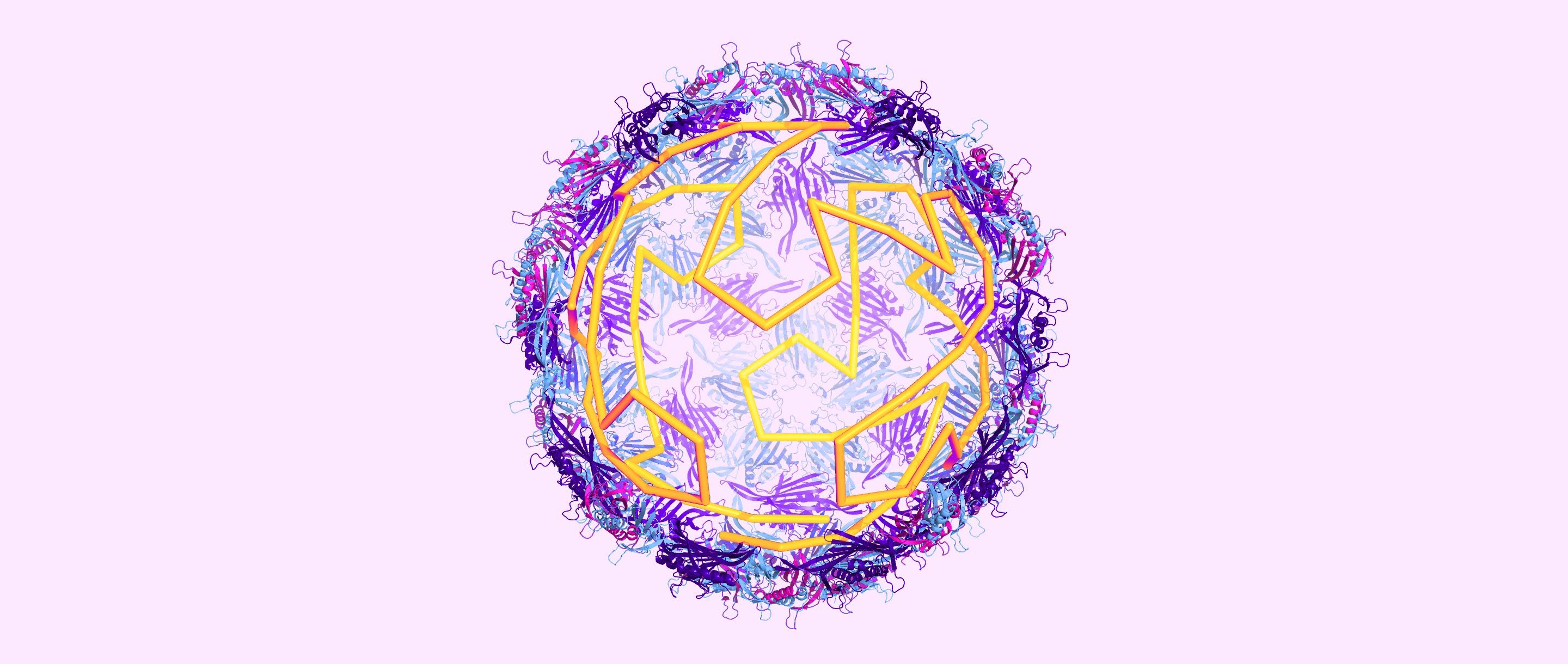
In 1962, the biologist-chemist duo Donald Caspar and Aaron Klug published a seminal paper on the structural organization of viruses. Among a series of sketches, models and X-ray diffraction patterns that the paper featured was a photograph of a building designed by Richard Buckminster Fuller, the inventor and architect: It was a geodesic dome, the design for which Fuller would become famous. And it was, in part, the lattice structure of the geodesic dome, a convex polyhedron assembled from hexagons and pentagons, themselves divided into triangles, that would inspire Caspar and Klug’s theory.

At the same time that Fuller was promoting the advantages of his domes — namely, that their structure made them more stable and efficient than other shapes — Caspar and Klug were trying to solve a structural problem in virology that had already attracted some of the field’s greats, not least among them James Watson, Francis Crick and Rosalind Franklin. Viruses consist of a short string of DNA or RNA packaged in a protein shell called a capsid, which protects the genomic material and facilitates its insertion into a host cell. Of course, the genomic material has to encode for the formation of such a capsid, and longer strands of DNA or RNA require larger capsids to shield them. It didn’t seem possible that strands as short as those found in viruses could achieve this.

Then, in 1956, three years after their work on DNA’s double helix, Watson and Crick came up with a plausible explanation. A viral genome could include instructions for only a limited number of distinct capsid proteins, which meant that in all likelihood viral capsids were symmetric: The genomic material needed to describe only some small subsection of the capsid and then give orders for it to be repeated in a symmetric pattern. Experiments using X-ray diffraction and electron microscopes revealed that this was indeed the case, making it apparent that viruses were predominantly either helical or icosahedral in shape. The former were rod-shaped structures that resembled an ear of corn, the latter polyhedra that approximated the sphere, consisting of 20 triangular faces glued together.

This 20-sided shape, one of the Platonic solids, can be rotated in 60 different ways without seeming to change in appearance. It also allows for the placement of 60 identical subunits, three on each triangular face, that are equally related to the symmetry axes — a setup that works perfectly for smaller viruses with capsids that consist of 60 proteins.

 

 

But most icosahedral viral capsids comprise a much larger number of subunits, and placing the proteins in this way never allows for more than 60. Clearly, a new theory was necessary to model larger viral capsids. That’s where Caspar and Klug entered the picture. Having recently read about Buckminster Fuller’s architectural creations, the pair realized it might have relevance to the structures of the viruses they were studying, which in turn sparked an idea. Dividing the icosahedron further into triangles (or, more formally, applying a hexagonal lattice to the icosahedron and then replacing each hexagon with six triangles) and positioning proteins in the corners of those triangles provided a more general and accurate picture of what these kinds of viruses looked like. This partitioning allowed for “quasi-equivalence,” in which subunits differ minimally in how they bond with their neighbors, forming either five-fold or six-fold positions on the lattice.

Such microscopic geodesic domes quickly became the standard way to represent icosahedral viruses, and, for a while, it seemed that Caspar and Klug had solved the problem. A handful of experiments conducted in the 1980s and ’90s, however, revealed some exceptions to the rule, most notably among groups of cancer-causing viruses called polyomaviridae and papillomaviridae.

It became necessary once more for an outside approach — made possible by theories in pure mathematics — to provide insights into the biology of viruses.

Following in Caspar and Klug’s Footsteps

About 15 years ago, Twarock came across a lecture about the different ways in which viruses realize their symmetrical structures. She thought she might be able to extend to these viruses some of the symmetry techniques she had been working on with spheres. “That snowballed,” Twarock said. She and her colleagues realized that with knowledge of structures, “we could make an impact on understanding how viruses function, how they assemble, how they infect, how they evolve.” She didn’t look back: She has spent her time since then working as a mathematical biologist, using tools from group theory and discrete math to continue where Caspar and Klug left off. “We really developed this integrative, interdisciplinary approach,” she said, “where the math drives the biology and the biology drives the math.”

Twarock first wanted to generalize the lattices that could be used so she could identify the positions of capsid subunits that Caspar and Klug’s work failed to explain. The proteins of the human papilloma viruses, for instance, were arranged in five-fold pentagonal structures, rather than hexagonal ones. Unlike hexagons, however, regular pentagons cannot be built from equilateral triangles, nor can they tessellate a plane: When slid next to each other to tile a surface, gaps and overlaps inevitably arise.

So Twarock turned to Penrose tilings, a mathematical technique developed in the 1970s to tile a plane with five-fold symmetry by fitting together four-sided figures called kites and darts. The patterns generated by Penrose tilings do not repeat periodically, making it possible to piece together its two component shapes without leaving any gaps. Twarock applied this concept by importing symmetry from a higher-dimensional space — in this case, from a lattice in six dimensions — into a three-dimensional subspace. This projection does not retain the periodicity of the lattice, but it does produce long-range order, like a Penrose tiling. It also encompasses the surface lattices used by Caspar and Klug. Twarock’s tilings therefore applied to a wider range of viruses, including the polyomaviruses and papillomaviruses that had evaded Caspar and Klug’s classification.

Moreover, Twarock’s constructions not only informed the locations and orientations of the capsid’s protein subunits, but they also provided a framework for how the subunits interacted with each other and with the genomic material inside. “I think this is where we made a very big contribution,” Twarock said. “By knowing about the symmetry of the container, you can understand better determinants of the asymmetric organization of the genomic material [and] constraints on how it must be organized. We were the first to actually float the idea that there should be order, or remnants of that order, in the genome.”

Twarock has been pursuing that line of research ever since.

The Role of Viral Genomes in Capsid Formation

Caspar and Klug’s theory applied only to the surfaces of capsids, not to their interiors. To know what was happening there, researchers had to turn to cryo-electron microscopy and other imaging techniques. Not so for Twarock’s tiling model, she said. She and her team set out hunting for combinatorial constraints on viral assembly pathways, this time using graph theory. In the process, they showed that in RNA viruses, the genomic material played a much more active role in the formation of the capsid than previously thought.

Specific positions along the RNA strand, called packaging signals, make contact with the capsid from inside its walls and help it form. Locating these signals with bioinformatics alone proves an incredibly difficult task, but Twarock realized she could simplify it by applying a classification based on a type of graph called a Hamiltonian path. Imagine the packaging signals as sticky pieces along the RNA string. One of them is stickier than the others; a protein will adhere to it first. From there, new proteins come into contact with other sticky pieces, forming an ordered pathway that never doubles back on itself. In other words, a Hamiltonian path.