Главная → Выпуск 7 → NewConcepts Chapters

History*

История математических обозначений

Март 2015
Опубликовано 2015-03-03 17:00

Математические обозначения — символы, используемые для компактной записи математических уравнений и формул. Помимо цифр и букв различных алфавитов (латинского, в том числе в готическом начертании, греческого и еврейского), математический язык использует множество специальных символов, изобретённых за последние несколько столетий.

Некоторые наиболее важные математические обзначения с указанием происхождения или изобретения их приводятся ниже.

От индийских значков, показанных в нижней строке (начертание I века н. э.), произошли современные цифры

$0123456789$

Для обозначения цифр от 1 до 9 в Индии с VI века до н. э. использовалось написание «брахми», с отдельными знаками для каждой цифры. Несколько видоизменившись, эти значки стали современными цифрами, которые мы называем арабскими, а сами арабы — индийскими.

Десятичная запятая, отделяющая дробную часть числа от целой, введена итальянским астрономом Маджини (1592) и Непером (1617). Ранее вместо запятой ставили иные символы — вертикальную черту: 3|62, или нуль в скобках: 3 (0) 62

«Двухэтажная» запись обыкновенной дроби (например $\ \frac {7}{12}\$ ) использовалась ещёдревнегреческими математиками, хотя знаменатель у них записывался надчислителем, а черты дроби не было. Индийские математики переместили числитель наверх; через арабов этот формат переняли в Европе. Дробную черту впервые в Европе ввёл Леонардо Пизанский (1202), но в обиход она вошла только при поддержке Иоганна Видмана (1489).

$\boldsymbol{+\;-}$

Знаки плюса и минуса придумали, по-видимому, в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в учебнике Иоганна Видмана «Быстрый и приятный счёт для всех торговцев», изданном в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m(minus)

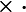
$\boldsymbol{\times \; \cdot}$

Знак умножения ввёл в 1631 году Уильям Отред (Англия) в виде косого крестика. До него использовали чаще всего букву M, хотя предлагались и другие обозначения: символ прямоугольника $\Box$ (Эригон, 1634), звёздочка (Иоганн Ран,1659). Позднее Лейбниц заменил крестик на точку (конец XVII века), чтобы не путать его с буквой x; до него такая символика встречалась у Региомонтана (XV век) и английского учёного Томаса Хэрриота (1560—1621).

$\boldsymbol{/ \; : \; \div}$

Знаки деления. Отред предпочитал косую черту. Двоеточием деление стал обозначать Лейбниц.

$\boldsymbol{\pm}$

Знак плюс-минус появился у Жирара (1626) и Отреда. Правда, Жирар между плюсом и минусом писал ещё словами «или».

$\boldsymbol{a^n}$

Возведение в степень. Современная запись показателя степени введена Декартом в его «Геометрии» (1637), правда, только для натуральных степеней, больших 2.

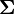
$\boldsymbol{\Sigma}$

Знак суммы ввёл Эйлер в 1755 году.

$\boldsymbol{\Pi}$

Знак произведения ввёл Гаусс в 1812 году.

$\boldsymbol{i}$

Букву i как код мнимой единицы: 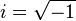$i=\sqrt{-1}$ предложил Эйлер (1777), взявший для этого первую букву слова imaginarius (мнимый).

$|x|$

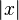
Обозначение абсолютной величины и модуля комплексного числа появились уВейерштрасса в 1841 году. В 1903 году Лоренц использовал эту же символику для длины вектора.

=
Первое печатное появление знака равенства (записано уравнение

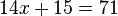14x + 15 = 71

)

Знак равенства предложил Роберт Рекорд в1557 году

$\approx$

Знак «приблизительно равно» придумал немецкий математик С. Гюнтер в 1882 году.

$\ne$

Знак «не равно» впервые встречается у Эйлера.

$\equiv$

Автор знака «тождественно равно» — Бернхард Риман (1857). Этот же символ, по предложению Гаусса, используется в теории чисел как знак сравнения по модулю, а в логике — как знак операции эквивалентности.

$<\ \ >$

Знаки сравнения ввёл Томас Хэрриот в своём сочинении, изданном посмертно в 1631 году. До него писали словами: больше, меньше.

$\leqslant\ \ \geqslant$

Символы нестрогого сравнения предложил Валлис в 1670 году.

$\angle$ , $\perp$

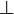
Символы «угол» и «перпендикулярно» придумал в 1634 году французский математик Пьер Эригон. Символ угла у Эригона напоминал значок $<$ , современную форму ему придал Уильям Отред (1657).

$30^\circ 40' 50''$

Современные обозначения угловых единиц (градусы, минуты, секунды) встречаются ещё в «Альмагесте» Птолемея. Радианную меру углов, более удобную для анализа, предложил в 1714 году английский математик Роджер Котс. Сам термин радиан придумал в 1873 году Джеймс Томсон, брат известного физика лорда Кельвина.

$\pi$

Общепринятое обозначение числа 3,14159… впервые образовал Уильям Джонс в1706 году, взяв первую букву слов греч. περιφρεια — окружность и περμετρος —периметр, то есть длина окружности. Это сокращение понравилось Эйлеру, труды которого закрепили обозначение окончательно.

$\sin, \cos$

Сокращённые обозначения для синуса и косинуса ввёл Отред в середине XVII века.

$\tan, \operatorname{tg}, \cot, \operatorname{ctg}$

Сокращённые обозначения тангенса и котангенса: $\operatorname{tg}, \operatorname{ctg}$ введены Иоганном Бернулли в XVIII веке, они получили распространение в Германии и России. В других странах употребляются названия этих функций $\tan, \cot$ , предложенные Альбером Жираром ещё ранее, в начале XVII века.

$\arcsin$

Манера обозначать обратные тригонометрических функции с помощью приставки arc (от лат. arcus, дуга) появилась у австрийского математика Карла Шерфера (нем. Karl Scherffer; 1716—1783) и закрепилась благодаряЛагранжу. Имелось в виду, что, например, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: $\sin^{-1}, \frac{1}{\sin}$ , но они не прижились.

$f'(x)$

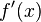
Манера обозначать производную по времени точкой над буквой идёт от Ньютона (1691).

Краткое обозначение производной штрихом восходит к Лагранжу.

$\int\limits_a^b f(x)\, dx$

Оформление определённого интеграла в привычном нам виде придумал Фурье.

$e$

Стандартное обозначение числа Эйлера e = 2,71828… предложено, естественно, Эйлером (1728, опубликовано в 1736 году).

$\frac{\partial}{\partial x}$

Символ частной производной сделали общеупотребительным сначала Карл Якоби (1837), а затем Вейерштрасс, хотя это обозначение уже встречалось ранее в одной работе Лежандра (1786).

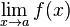
$\lim_{x \to a} f(x)$

Символ предела появился в 1787 году у Симона Люилье и получил поддержку Коши (1821)^[9]. Предельное значение аргумента сначала указывалось отдельно, после символа lim, а не под ним. Близкое к современному обозначение ввёл Вейерштрасс, однако вместо привычной нам стрелки он использовал знак равенства^[10]. Стрелка появилась в начале XX века сразу у нескольких математиков — например, у Харди (1908).

$\nabla$

Символ этого дифференциального оператора придумал Уильям Роуэн Гамильтон(1853), а название «набла» предложил Хевисайд (1892).

Полный список математических обозначений с указанием истории их возникновения - в статье Википедии ИСТОРИЯ МАТЕМАТИЧЕСКИХ ОБОЗНАЧЕНИЙ

находящейся на интернете в свободном доступе

http://goo.gl/WcU0Ss

Добавить комментарий

Оставлять комментарии могут только зарегистрированные пользователи. Войдите в систему используя свою учетную запись на сайте:
Email: Пароль:	напомнить пароль Регистрация